Regularity In Math Examples - The standard definition of regularity goes like this: Look for and express regularity in repeated reasoning. $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. This includes all rational functions, which are built up from combinations of the function x with. Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various flavours of the theory of (controlled) rough paths (including. While many problems or tasks do require students to use a combination of. The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness of a domain boundary, the. Every elementary function is continuous. A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved.
Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various flavours of the theory of (controlled) rough paths (including. $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. Look for and express regularity in repeated reasoning. While many problems or tasks do require students to use a combination of. The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness of a domain boundary, the. Every elementary function is continuous. This includes all rational functions, which are built up from combinations of the function x with. The standard definition of regularity goes like this:
Look for and express regularity in repeated reasoning. This includes all rational functions, which are built up from combinations of the function x with. The standard definition of regularity goes like this: Every elementary function is continuous. While many problems or tasks do require students to use a combination of. Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various flavours of the theory of (controlled) rough paths (including. $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness of a domain boundary, the.
(PDF) A regularity theory for an initial value problem with a time
A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. While many problems or tasks do require students to use a combination of. $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various.
Global regularity for systems with symmetric gradients
Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various flavours of the theory of (controlled) rough paths (including. This includes all rational functions, which are built up from combinations of the function x with. Look for and express regularity in repeated reasoning. While many problems or tasks do require students to use a combination of. A.
The Common Fixed Point Theorems for Asymptotic Regularity on bMetric
A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. The standard definition of regularity goes like this: While many problems or tasks do require students to use a combination of. Every elementary function is continuous. The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness.
Regularity Regularity in Language Regularity in Pragmatics YouTube
Every elementary function is continuous. While many problems or tasks do require students to use a combination of. $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. This includes all rational functions, which are built up from combinations of the function x with. The regularity a solution can inherit depends on the properties.
(PDF) {\mathscr {A}}quasiconvexity and partial regularity
A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. Every elementary function is continuous. While many problems or tasks do require students to use a combination of. $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. This includes all rational functions, which are built.
Pattern and Regularities Mathematics in the Modern World YouTube
The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness of a domain boundary, the. A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. Every elementary function is continuous. The standard definition of regularity goes like this: Very recently, a new theory of “regularity structures”.
Look for and Express Regularity in Repeated Reasoning… in Math!
$m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. While many problems or tasks do require students to use a combination of. The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness of a domain boundary, the. This includes all rational functions, which are built up from.
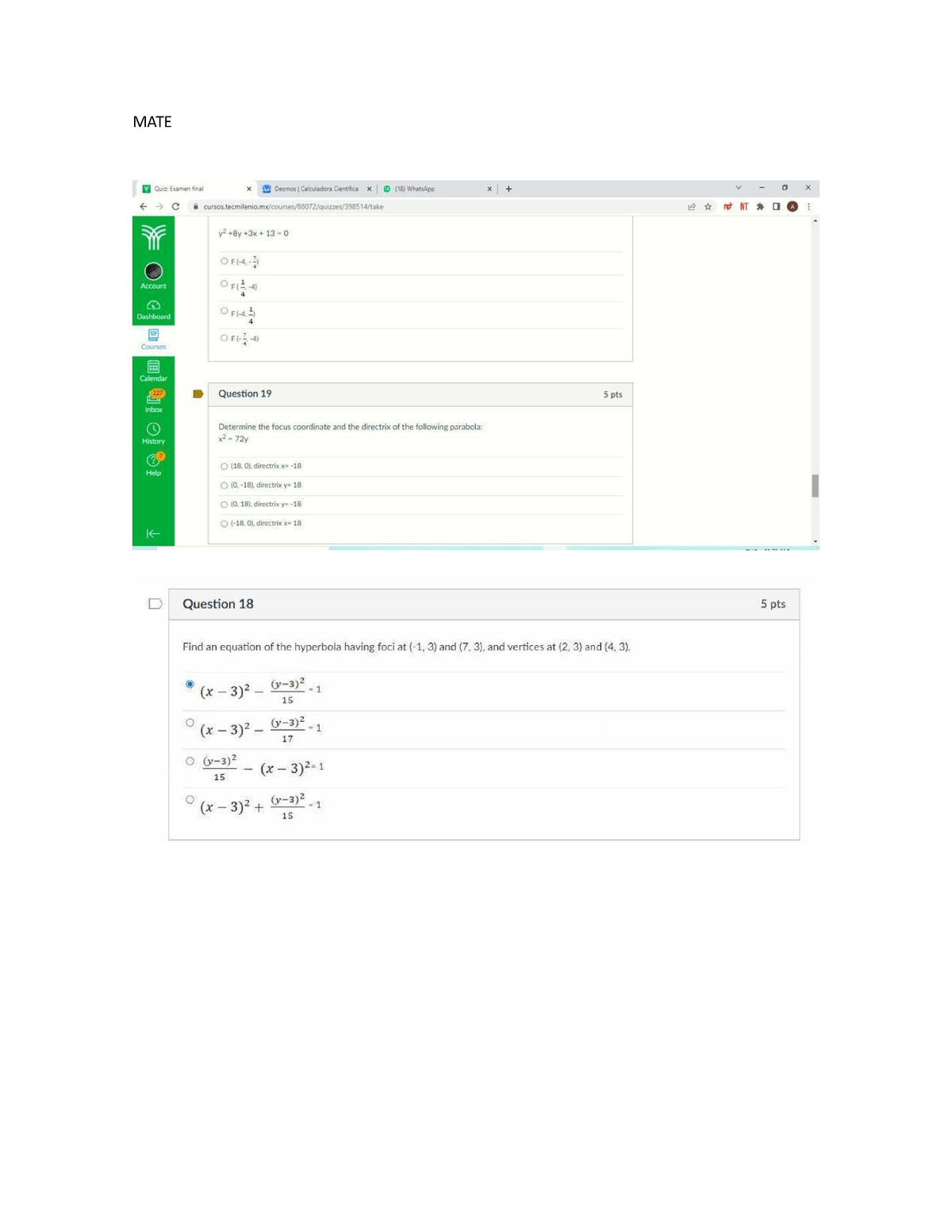
MATE Examen Final EXAM Math III regularity and repetition MATE
The standard definition of regularity goes like this: This includes all rational functions, which are built up from combinations of the function x with. Every elementary function is continuous. While many problems or tasks do require students to use a combination of. $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures.
Regularity form OHM VITAL
This includes all rational functions, which are built up from combinations of the function x with. A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness of a domain boundary, the. Look for and express regularity.
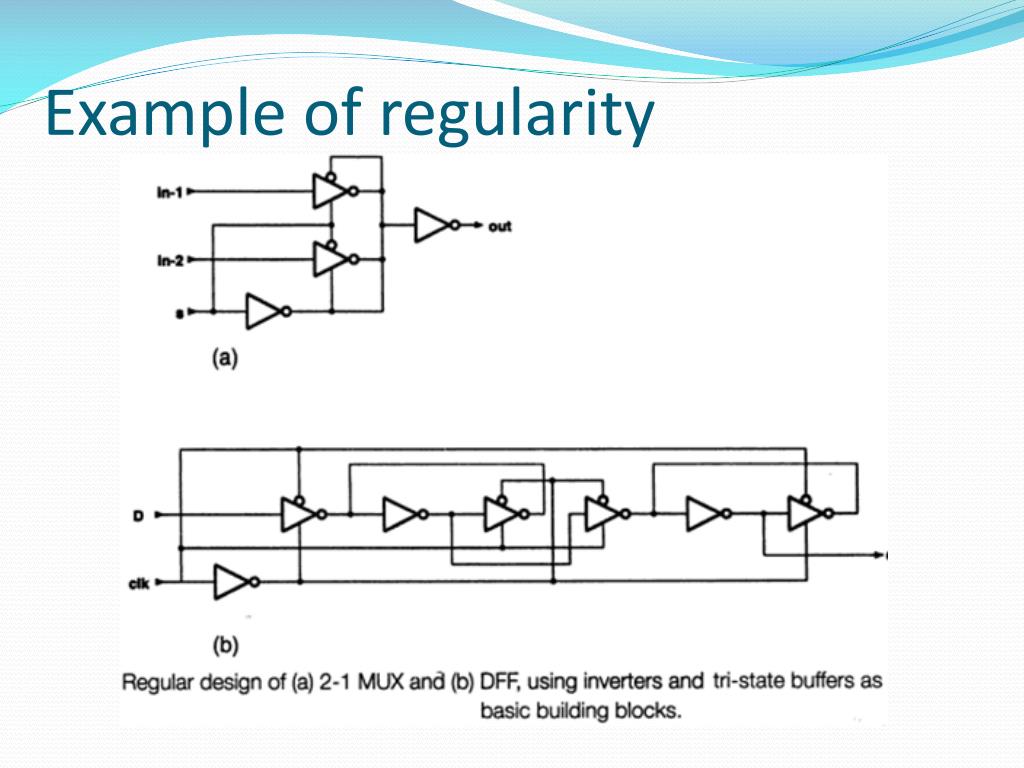
PPT Chapter 1 PowerPoint Presentation, free download ID1587802
The standard definition of regularity goes like this: A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. This includes all rational functions, which are built up from combinations of the function x with. Every elementary function is continuous. While many problems or tasks do require students to use a combination of.
A Regularity Condition Is Essentially Just A Requirement That Whatever Structure You Are Studying Isn't Too Poorly Behaved.
This includes all rational functions, which are built up from combinations of the function x with. Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various flavours of the theory of (controlled) rough paths (including. $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. While many problems or tasks do require students to use a combination of.
Every Elementary Function Is Continuous.
The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness of a domain boundary, the. Look for and express regularity in repeated reasoning. The standard definition of regularity goes like this: