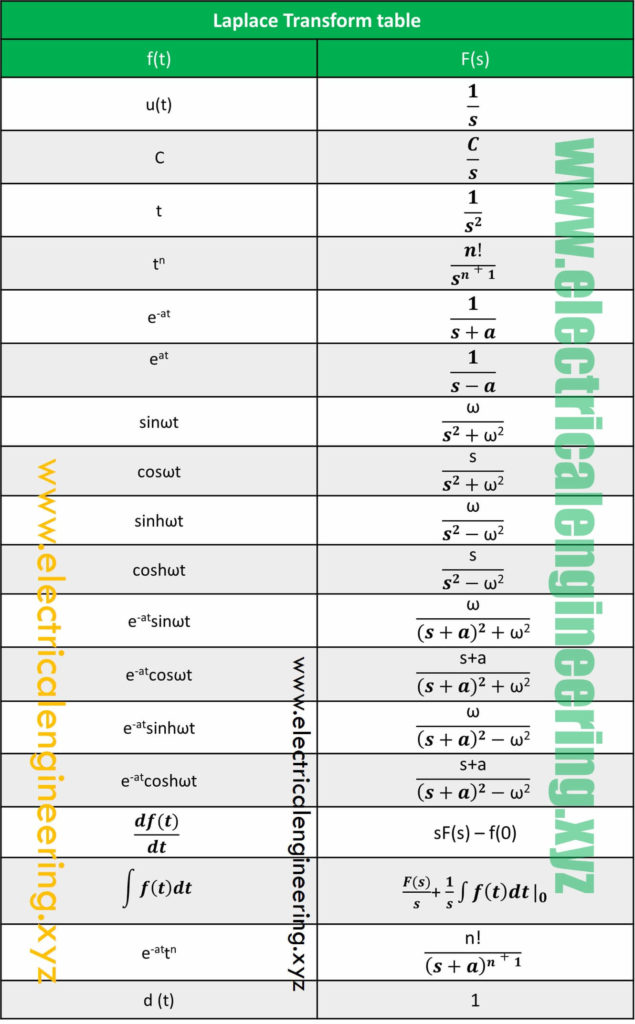
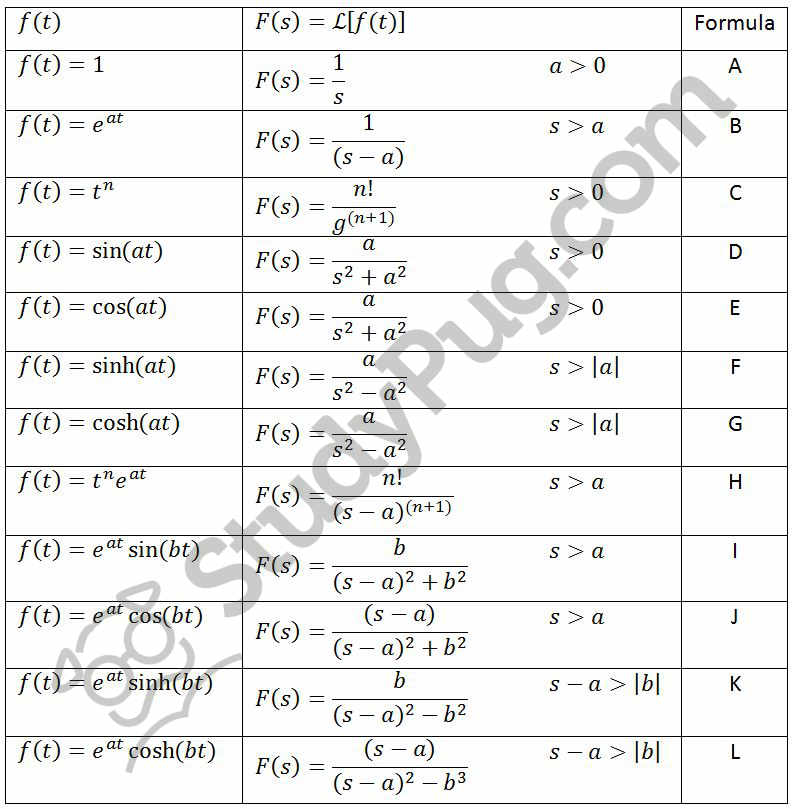
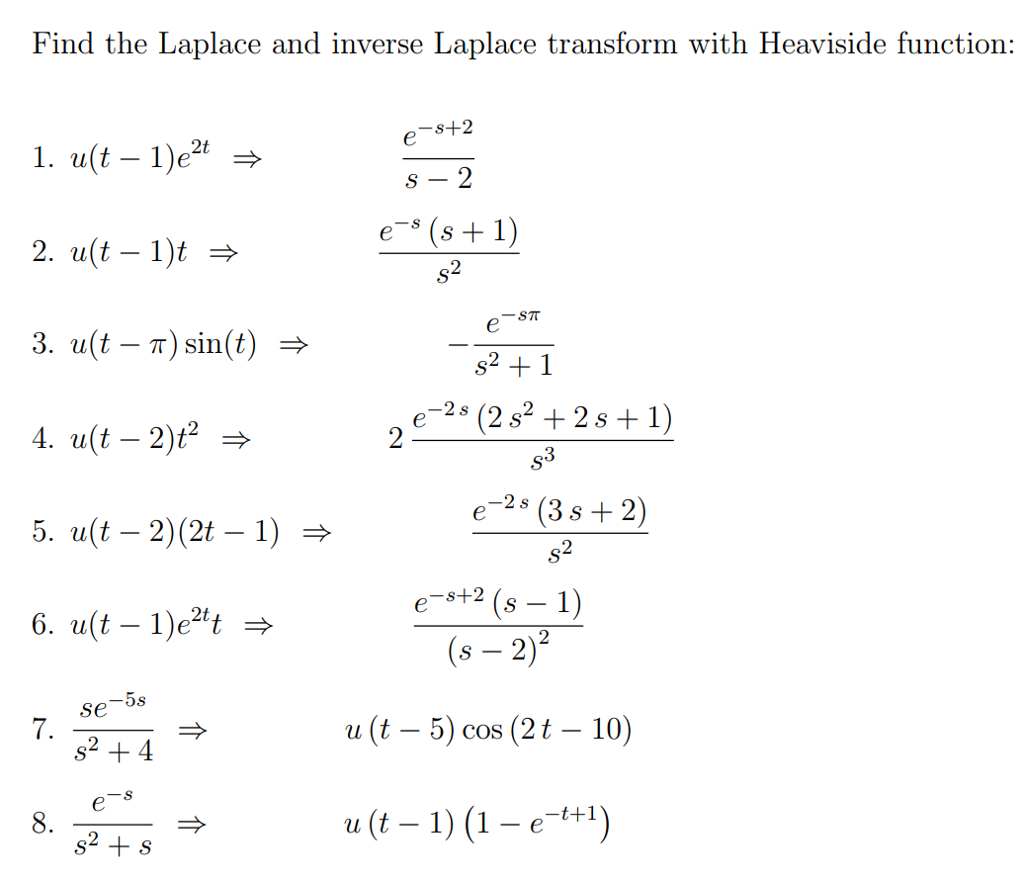Laplace Transform Sheet - In these two examples the functions f and g are the same except at t = 0, so they have the same laplace transform. Sn+1 4.tp (p>−1) γ(p+1) sp+1 5. Laplace transform table f(t)=l−1{f(s)} f(s)=l{f(t)} 1. In the ̄rst case, f has no jump at t = 0,. Solve y′′+ 3y′−4y= 0 with y(0) = 0 and y′(0) = 6, using the laplace transform. 1 1 s 2.eat 1 s−a 3.tn n! Sinat a s 2+a 6. (b) use rules and solve:. Table of laplace transforms f(x) f(s) = l[f(x)] c c s, s > 0 erx 1 s−r, s > r cos βx s s2 +. Table of laplace transforms f(t) l[f(t)] = f(s) 1 1 s (1) eatf(t) f(s a) (2) u(t a) e as s (3) f(t a)u(t a) e asf(s) (4) (t) 1 (5) (t stt 0) e 0 (6) tnf(t) ( 1)n dnf(s).
Cosat s s 2+a 7. Sn+1 4.tp (p>−1) γ(p+1) sp+1 5. Sinat a s 2+a 6. Table of laplace transforms f(t) l[f(t)] = f(s) 1 1 s (1) eatf(t) f(s a) (2) u(t a) e as s (3) f(t a)u(t a) e asf(s) (4) (t) 1 (5) (t stt 0) e 0 (6) tnf(t) ( 1)n dnf(s). Table of laplace transforms f(x) f(s) = l[f(x)] c c s, s > 0 erx 1 s−r, s > r cos βx s s2 +. 1 1 s 2.eat 1 s−a 3.tn n! Laplace transform table f(t)=l−1{f(s)} f(s)=l{f(t)} 1. Solve y′′+ 3y′−4y= 0 with y(0) = 0 and y′(0) = 6, using the laplace transform. In the ̄rst case, f has no jump at t = 0,. (b) use rules and solve:.
Cosat s s 2+a 7. Laplace transform table f(t)=l−1{f(s)} f(s)=l{f(t)} 1. In the ̄rst case, f has no jump at t = 0,. In these two examples the functions f and g are the same except at t = 0, so they have the same laplace transform. Table of laplace transforms f(x) f(s) = l[f(x)] c c s, s > 0 erx 1 s−r, s > r cos βx s s2 +. (b) use rules and solve:. Sinat a s 2+a 6. Solve y′′+ 3y′−4y= 0 with y(0) = 0 and y′(0) = 6, using the laplace transform. Sn+1 4.tp (p>−1) γ(p+1) sp+1 5. Table of laplace transforms f(t) l[f(t)] = f(s) 1 1 s (1) eatf(t) f(s a) (2) u(t a) e as s (3) f(t a)u(t a) e asf(s) (4) (t) 1 (5) (t stt 0) e 0 (6) tnf(t) ( 1)n dnf(s).
Solved Use Laplace Transforms To Solve The Initial Value
Laplace transform table f(t)=l−1{f(s)} f(s)=l{f(t)} 1. (b) use rules and solve:. Sinat a s 2+a 6. Table of laplace transforms f(t) l[f(t)] = f(s) 1 1 s (1) eatf(t) f(s a) (2) u(t a) e as s (3) f(t a)u(t a) e asf(s) (4) (t) 1 (5) (t stt 0) e 0 (6) tnf(t) ( 1)n dnf(s). 1 1 s.
laplacetransformtableformulasheet • Electrical Engineering XYZ
Sn+1 4.tp (p>−1) γ(p+1) sp+1 5. Table of laplace transforms f(x) f(s) = l[f(x)] c c s, s > 0 erx 1 s−r, s > r cos βx s s2 +. 1 1 s 2.eat 1 s−a 3.tn n! In the ̄rst case, f has no jump at t = 0,. Cosat s s 2+a 7.
Inverse Laplace Transform Practice Sheet
Table of laplace transforms f(t) l[f(t)] = f(s) 1 1 s (1) eatf(t) f(s a) (2) u(t a) e as s (3) f(t a)u(t a) e asf(s) (4) (t) 1 (5) (t stt 0) e 0 (6) tnf(t) ( 1)n dnf(s). Sinat a s 2+a 6. 1 1 s 2.eat 1 s−a 3.tn n! In the ̄rst case, f has.
BA501ENGINEERING MATHEMATICS 4 CHAPTER 5 JKELAPLACE TRANSFORM
In the ̄rst case, f has no jump at t = 0,. 1 1 s 2.eat 1 s−a 3.tn n! (b) use rules and solve:. Table of laplace transforms f(x) f(s) = l[f(x)] c c s, s > 0 erx 1 s−r, s > r cos βx s s2 +. Cosat s s 2+a 7.
Inverse laplace transforms StudyPug
Cosat s s 2+a 7. Laplace transform table f(t)=l−1{f(s)} f(s)=l{f(t)} 1. Sn+1 4.tp (p>−1) γ(p+1) sp+1 5. In these two examples the functions f and g are the same except at t = 0, so they have the same laplace transform. Table of laplace transforms f(t) l[f(t)] = f(s) 1 1 s (1) eatf(t) f(s a) (2) u(t a) e.
لاپلاس و معکو س آن
Table of laplace transforms f(x) f(s) = l[f(x)] c c s, s > 0 erx 1 s−r, s > r cos βx s s2 +. Table of laplace transforms f(t) l[f(t)] = f(s) 1 1 s (1) eatf(t) f(s a) (2) u(t a) e as s (3) f(t a)u(t a) e asf(s) (4) (t) 1 (5) (t stt 0) e.
Calculating laplace transforms StudyPug in 2024
Solve y′′+ 3y′−4y= 0 with y(0) = 0 and y′(0) = 6, using the laplace transform. Sn+1 4.tp (p>−1) γ(p+1) sp+1 5. 1 1 s 2.eat 1 s−a 3.tn n! Laplace transform table f(t)=l−1{f(s)} f(s)=l{f(t)} 1. Cosat s s 2+a 7.
Table of Laplace Transforms Cheat Sheet by Cheatography Download free
Cosat s s 2+a 7. (b) use rules and solve:. Laplace transform table f(t)=l−1{f(s)} f(s)=l{f(t)} 1. Table of laplace transforms f(t) l[f(t)] = f(s) 1 1 s (1) eatf(t) f(s a) (2) u(t a) e as s (3) f(t a)u(t a) e asf(s) (4) (t) 1 (5) (t stt 0) e 0 (6) tnf(t) ( 1)n dnf(s). 1 1 s.
SOLUTION Laplace transform and inverse laplace transform formula sheet
Table of laplace transforms f(t) l[f(t)] = f(s) 1 1 s (1) eatf(t) f(s a) (2) u(t a) e as s (3) f(t a)u(t a) e asf(s) (4) (t) 1 (5) (t stt 0) e 0 (6) tnf(t) ( 1)n dnf(s). (b) use rules and solve:. Laplace transform table f(t)=l−1{f(s)} f(s)=l{f(t)} 1. In the ̄rst case, f has no jump.
[Solved] Using the Laplace transform pairs in the formula sheet
Cosat s s 2+a 7. Sn+1 4.tp (p>−1) γ(p+1) sp+1 5. Table of laplace transforms f(x) f(s) = l[f(x)] c c s, s > 0 erx 1 s−r, s > r cos βx s s2 +. 1 1 s 2.eat 1 s−a 3.tn n! (b) use rules and solve:.
Solve Y′′+ 3Y′−4Y= 0 With Y(0) = 0 And Y′(0) = 6, Using The Laplace Transform.
Sinat a s 2+a 6. Table of laplace transforms f(x) f(s) = l[f(x)] c c s, s > 0 erx 1 s−r, s > r cos βx s s2 +. Cosat s s 2+a 7. Table of laplace transforms f(t) l[f(t)] = f(s) 1 1 s (1) eatf(t) f(s a) (2) u(t a) e as s (3) f(t a)u(t a) e asf(s) (4) (t) 1 (5) (t stt 0) e 0 (6) tnf(t) ( 1)n dnf(s).
(B) Use Rules And Solve:.
In the ̄rst case, f has no jump at t = 0,. In these two examples the functions f and g are the same except at t = 0, so they have the same laplace transform. 1 1 s 2.eat 1 s−a 3.tn n! Sn+1 4.tp (p>−1) γ(p+1) sp+1 5.